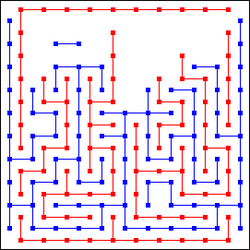
Bridg-It
Bridg-It, also known as Gale, is a connection game, similar to Hex. It was invented by the mathematician David Gale, and was described, under the name "Gale", in Martin Gardner's October 1958 column in Scientific American. A version was later marketed by Hasbro under the name "Bridg-It".
Contents
Rules
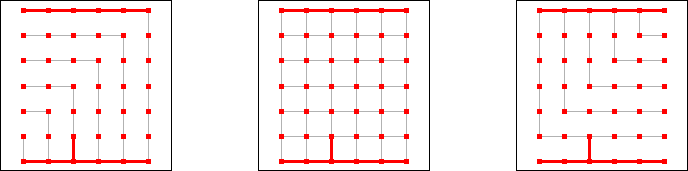
The game is played on a square board. One player (Blue) tries to connect the West and East side, the other tries to connect the North and South side of the board. In each turn, a player draws either a horizontal or a vertical line. Red's lines don't end at the same coordinates as Blue's lines, rather their center points are the same. Lines must not cross each other, which means that every center point can only be occupied by one of the players.
Observations
The game cannot end in a draw.
The game of Bridg-It is equivalent to a special case of Hex where some of the cells are already filled in at the start of the game. For example, 6x6 Brid-it, shown on the right, is equivalent to the following Hex position:
However, since this position never arises during a normal game of Hex, the usual elements of Hex strategy (such as templates, ladder escapes, etc.) do not necessarily apply to Bridg-It.
The first player has a theoretical winning strategy in Bridg-It, for the same reason as in Hex.
Bridg-It is a special case of the Shannon (edge) switching game, for which an optimal move can be found in polynomial time using matroid theory. In other words, the game is solved.
Winning strategy
An explicit winning strategy
An explicit first-player winning strategy for Bridg-It is known. In fact, we can describe a strategy by which Red will connect all vertices by red paths, not just the top and bottom. It can be described as follows. We use 6x6 Bridg-It as an example, but the same strategy works for any (square) size.
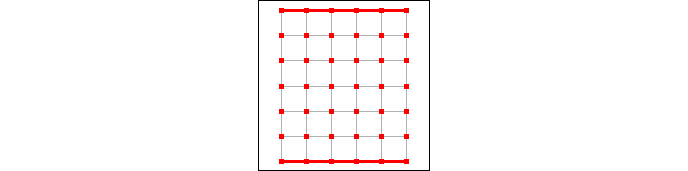
We first re-formulate Bridg-It as an edge Shannon game. When seen in this way, the game is played on the following graph:
The two players, Red and Blue, alternate. On Red's turn, Red colors one of the grey edges red. On Blue's turn, Blue erases one of the grey edges. Red wins if there is a red path connecting the top and bottom. This formulation is equivalent to the original Bridg-It; the only difference is that Blue erases edges, rather than crossing them out.
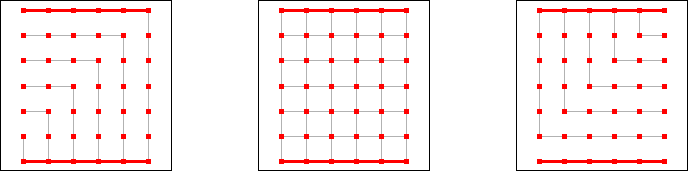
To describe Red's strategy, we keep track of three graphs. All three graphs have the same vertices. Initially, they are the following:
The middle graph is the one the actual game is played on. The left and right graphs have the same red edges as the middle graph, but each grey edge is only present in exactly one of the left or right graphs. We note that the left graph is a tree (i.e., there is a unique path between any two vertices), and the right graph is the union of two trees (i.e., it has exactly two connected components, each of which is a tree).
Red plays as follows. Each time it is Red's turn, Red checks which of the two graphs (left or right) is disconnected. Red then picks an edge in the opposite graph (right or left) that connects the two disconnected components of the disconnected graph. (Such an edge always exists because the opposite graph is connected). Red colors this edge red in all three graphs (and in particular makes a move in the middle game). After Red's move, both the left and right graphs are trees.
When it is Blue's turn, Blue erases one of the grey edges in the middle graph. We erase the corresponding grey edge in the left or right graph as well. Therefore, at the end of Blue's turn, exactly one of the left or right graphs is disconnected (a union of two trees), and the other is a tree.
Now Red checks again which of the graphs is disconnected (it is again the right one). Red picks an edge from the left graph that will reconnect the right graph, and colors it red in all three graphs.
The game continues in this way until there are no more grey edges. At this point, all three graphs are the same. Since one of them is a tree, all three of them are, i.e., Red has connected all vertices.
Every opening move is winning
The above explicit strategy shows that every vertical opening move on the bottom row is winning for Red. It is not difficult to generalize this to show that in fact every opening move is winning. One just needs to start with a different partition of the grey edges into a spanning tree and an almost-spanning-tree.
A consequence of this is that it does not make much sense to apply the swap rule to Bridg-It. No matter the opening move, the opponent should always swap.
Commercial version
A commercial version of Bridg-It was marketed by Hassenfeld Brothers (Hasbro) in 1960. This version came with a 5x5 grid and 20 bridges for each player. The rules suggested that when a player runs out of bridges, they continue playing by picking up an already placed bridge and moving it elsewhere. This is not quite the same as the original game, where players have an unlimited number of bridges and they are never moved.
Playing online
- A Java implementation of Bridg-It by Roland Illig, using the name "Connecto": http://roland-illig.de/lang.java.connecto.html
References
- Sandy Dean, The Game of Bridg-It. M.A. thesis, Department of Mathematics, University of Nebraska-Lincoln, July 2008.
- Ryan Hayward and Bjarne Toft. Hex: The Full Story. CRC Press, 2019. ISBN 978-0367144227. Sections 6.4, 8.1, and 8.2 discuss Bridg-It.
- Martin Gardner. Mathematical games: Four mathematical diversions involving concepts of topology. Scientific American, Vol. 199, No. 4 (October 1958), pp. 124–129.