User:Bobson8

7th row single-stone pre-template

The following pattern guarantees a stone on 7th row to connect to the edge. It was verified by me using HexProver developped by mirefek. Whether this connection is minimal is not known. This partially answers the single-stone 7th row edge template problem (The template exists but the shape is unknown).

To start with, one notice that Red can connect to the edge with a variant of edge template V1b from both sides.

Thus Blue has these possible blocks (a~j, mirrored positions are removed).

For Blue playing a,b,c,d, Red can respond with X,Y,Y,Z respectively. For the rest Red can respond with b.

A conjecture on Trapezoid boards

Conjecture. For an isosceles trapezoid board of edge lengths a (Red), b (Blue), a+b-1 (Red), b (Blue),

(1) "Red always loses regardless of who goes first" if and only if b >= 2a+1 (In other words, Red's average edge length <= Blue's-1).

(2) "Red always wins regardless of who goes first" if and only if b <= 2a-3 (In other words, Red's average edge length >= Blue's+1).

Indeed, this conjecture is an analog of the results on parallelogram boards. I have verified this conjecture for a=1,2,3, and KataHex suggested that a=4,5,6 are possibly true.

To prove this conjecture one need to verify

(1) When b=2a-3, Red wins even if Blue goes first.

(2) When b=2a-2, Red loses if Blue goes first.

(3) When b=2a, Red wins if Red goes first.

(4) When b=2a+1, Red loses even if Red goes first.

We demo some small cases (a=1,2,3).

(a,b)=(1,2): Red wins with a bridge.

(a,b)=(1,3): Blue edges form a span template.

(a,b)=(2,1): Red edges form a bridge template.

(a,b)=(2,2): Blue wins with a chain of two bridges.

(a,b)=(2,4): Red wins with a chain of a bridge and a ziggurat.

(a,b)=(2,5): Blue edges form a template. One possible defence for Red:

(a,b)=(3,3): Red edges are connected by the edge template IV2a.

(a,b)=(3,4): Blue wins with a chain of two ziggurats.

(a,b)=(3,6): Red can win with this template:

(a,b)=(3,7): Blue edges form a pre-template. There are two template within it, removing cells either with * or with + (due to Quasar). When Red plays 1, Blue can play at a for the * case, or b for the + case:

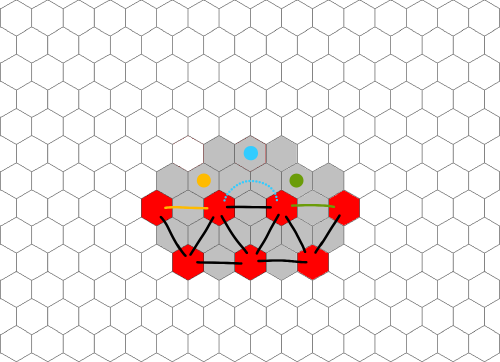
Some interior templates

These templates assume that one has to connect all the red pieces on the boundaries. (The middle pieces are also gauranteed to be connected, though insignificant in practice.)

This template can be verified by the disjoint spanning tree theorem (the criterion being used in the Shannon switching game).

Removing a Red terminal on a corner from the previous template still gives a template.

A strategy for this template could be intepreted as the Shannon switching game on this graph of 7 vertices and 12 edges. There is an exceptional rule for this game: Red can save the dotted edge only after the yellow and green edges have been played by any player.

When the dotted edge have not been played, Red can save the yellow edge by playing a red piece at the yellow spot and connect the two parts with a bridge. If Blue breaks the yellow edge by playing a blue piece on it, then Red can also automatically peep at the yellow spot. The same applies to green.

In any other cases, If Blue plays inside the tunnel, then they are considered breaking the dotted edge. Red can save the dotted edge by playing a red piece on the cyan spot and connect to the yellow and green spots with bridges.

This switching game itself is not obviously winning for Red. One has to check case by case.